| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
- 정기 코딩 인증평가
- 카카오
- 백준
- 오블완
- 핵심
- 해결
- 등산코스 정하기
- 수료
- 티스토리챌린지
- 퍼즐 조각 채우기
- 카카오코드 본선
- 프로그래머스
- 배열 돌리기 5
- 10기
- 설명
- java
- 142085
- PCCP
- 산 모양 타일링
- SQL
- 인턴십
- 싸피
- MySQL
- 후기
- SSAFY
- softeer
- 숫자 이어 붙이기
- 소프티어
- 14942
- 24955
- Today
- Total
개발 쥬스
[핵심정리] 크루스칼 알고리즘 본문
크루스칼 알고리즘에 대해서 핵심만 담아보았습니다.
시간복잡도: O(ElogE) (E: 그래프의 간선의 개수)
크루스칼 알고리즘을 알기 전에 먼저 다음 개념을 알아야 합니다.
🔍 신장 트리란?
하나의 그래프가 있을 때 모든 노드를 포함하면서 사이클이 존재하지 않는 부분 그래프를 의미합니다.
위 개념을 바탕으로 크루스칼 알고리즘에 대한 설명을 하면 다음과 같습니다.
🔍 크루스칼 알고리즘이란?
그리디 알고리즘으로 분류되고 가장 적은 비용으로 만든 신장 트리를 의미합니다.
그렇다면 크루스칼 알고리즘은 어떻게 구현하는지 그림을 통해서 원리를 파악하겠습니다.
🔍 크루스칼 알고리즘의 구현 과정
핵심은 그래프에서 서로 연결되어 있는 간선의 비용이 가장 작은 선들을 우선적으로 선택하고, 간선을 구성하고 있는 노드들을 서로 집합에 포함시켜가며 사이클을 유발하는 부분을 제거해나가면 됩니다.
그림과 같이 다음 그래프를 가지고 크루스칼 알고리즘을 적용해보겠습니다.
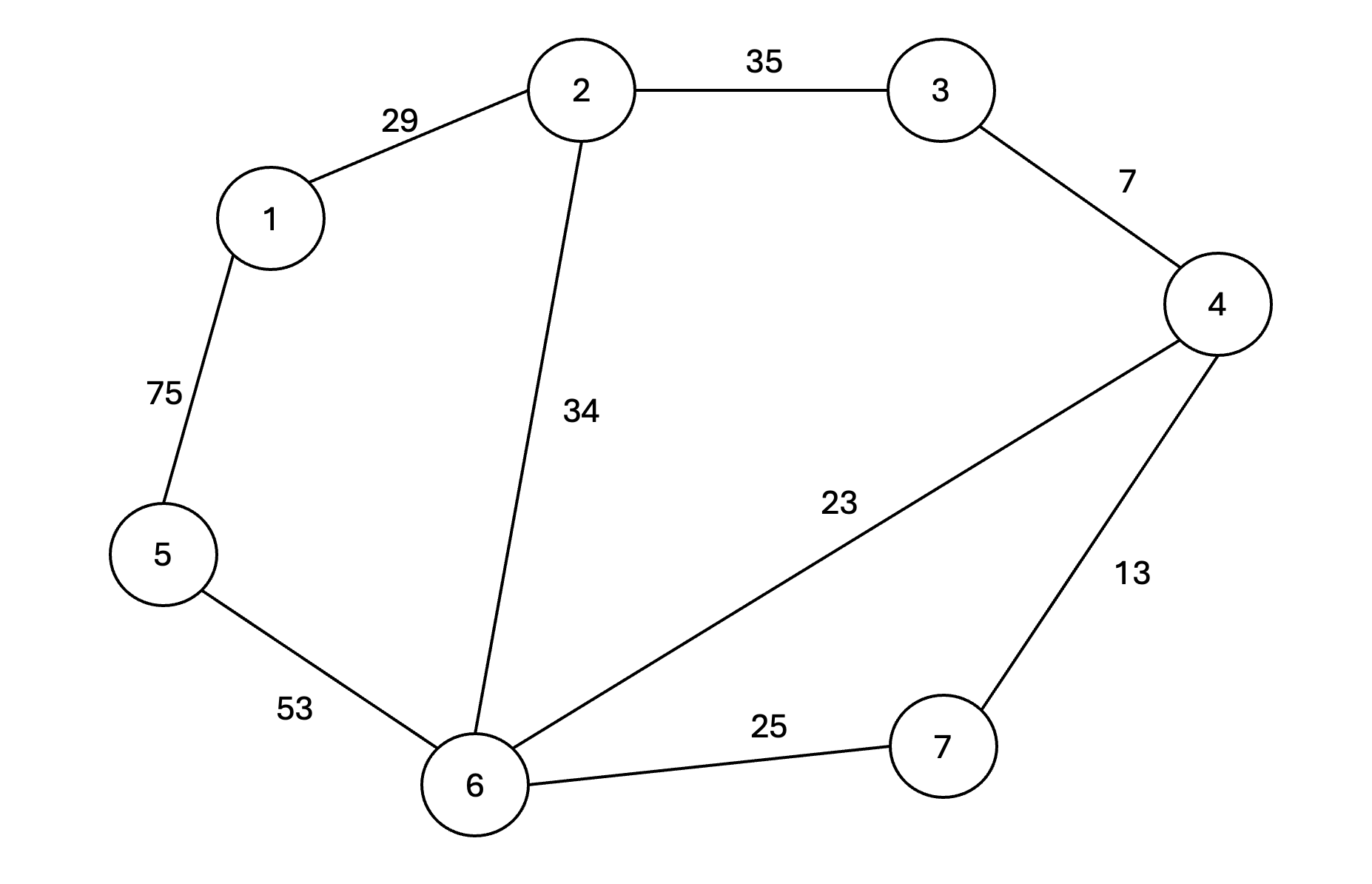
그리고 간선과 비용 정보를 담은 테이블은 다음과 같습니다.
| 간선 | (1, 2) | (1, 5) | (2, 3) | (2, 6) | (3, 4) | (4, 6) | (4, 7) | (5, 6) | (6, 7) |
| 비용 | 29 | 75 | 35 | 34 | 7 | 23 | 13 | 53 | 25 |
1️⃣ 비용들 중에서 가장 작은 비용을 가진 간선을 우선적으로 선택합니다. 노드 3과 4의 비용은 7이므로 이 둘에 대해서 집합에 포함시킵니다. 그래프의 변화는 없습니다.
| 간선 | (1, 2) | (1, 5) | (2, 3) | (2, 6) | (3, 4) | (4, 6) | (4, 7) | (5, 6) | (6, 7) |
| 비용 | 29 | 75 | 35 | 34 | 7 | 23 | 13 | 53 | 25 |
| 순서 | step 1 |
현재 존재하는 집합: (3, 4)
2️⃣ 그 다음 짧은 간선은 노드 4와 노드 7이 연결된 간선입니다. 이 둘을 집합에 포함시킵니다. 마찬가지로 그래프의 상태 변화는 없습니다.
| 간선 | (1, 2) | (1, 5) | (2, 3) | (2, 6) | (3, 4) | (4, 6) | (4, 7) | (5, 6) | (6, 7) |
| 비용 | 29 | 75 | 35 | 34 | 7 | 23 | 13 | 53 | 25 |
| 순서 | step 1 | step 2 |
현재 존재하는 집합: (3, 4, 7)
3️⃣ 다음으로 노드 4와 노드 6이 연결된 간선을 선택하고 이 둘 노드를 집합에 포함시킵니다.
| 간선 | (1, 2) | (1, 5) | (2, 3) | (2, 6) | (3, 4) | (4, 6) | (4, 7) | (5, 6) | (6, 7) |
| 비용 | 29 | 75 | 35 | 34 | 7 | 23 | 13 | 53 | 25 |
| 순서 | step 1 | step 3 | step 2 |
현재 존재하는 집합: (3, 4, 6, 7)
4️⃣ 다음으로 4와 6이 연결된 간선을 살펴봅니다. 그런데 4와 6은 이미 같은 집합에 속해있기에 이 간선은 선택할 수가 없습니다. 따라서 그래프에서 해당 간선은 제거됩니다.
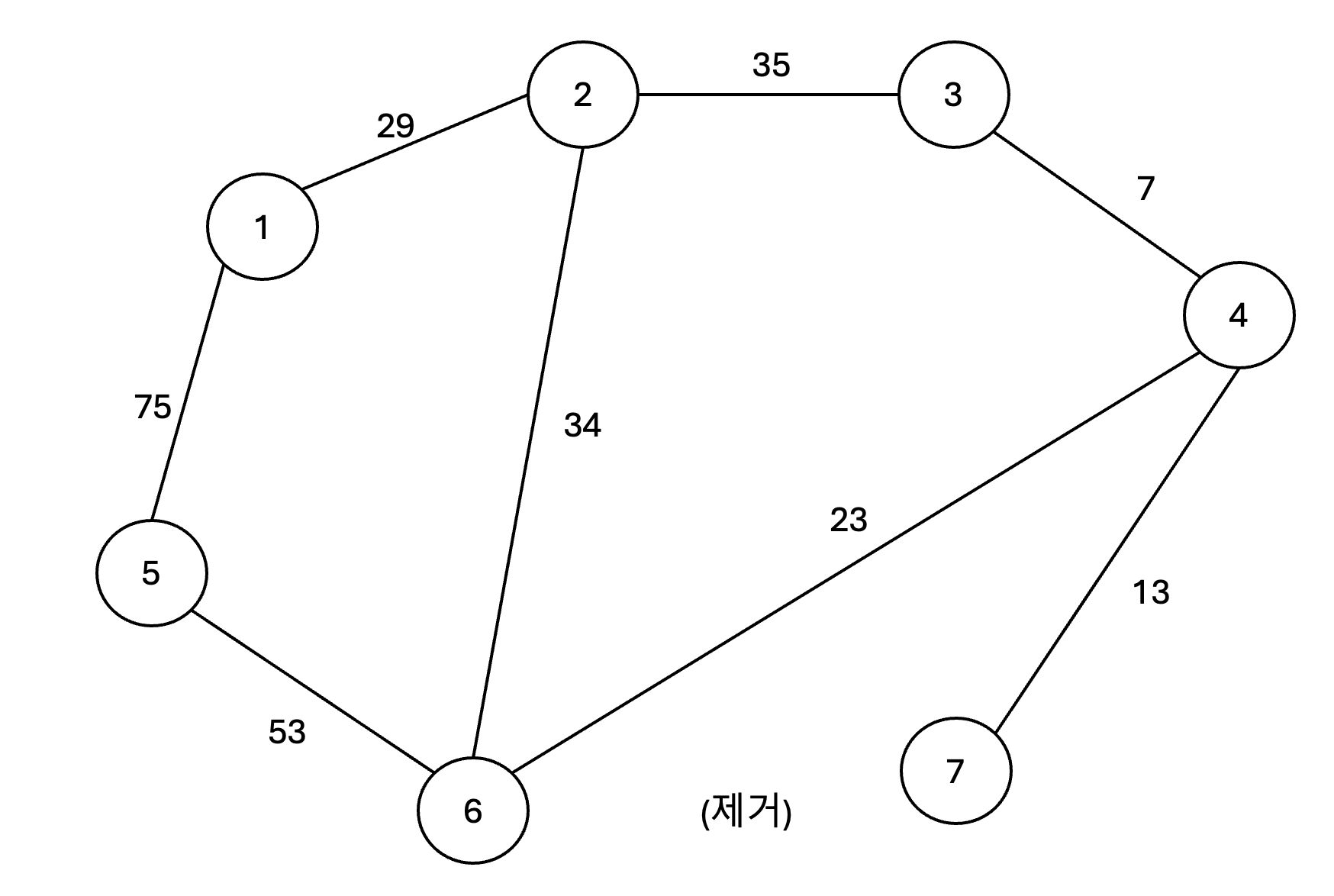
| 간선 | (1, 2) | (1, 5) | (2, 3) | (2, 6) | (3, 4) | (4, 6) | (4, 7) | (5, 6) | (6, 7) |
| 비용 | 29 | 75 | 35 | 34 | 7 | 23 | 13 | 53 | 25 |
| 순서 | step 1 | step 3 | step 2 | step 4 |
현재 존재하는 집합: (3, 4, 6, 7)
5️⃣ 노드 1과 노드 2의 간선을 선택합니다. 1과 2는 같은 집합에 속해 있지 않으므로 집합에 포함시킵니다.
| 간선 | (1, 2) | (1, 5) | (2, 3) | (2, 6) | (3, 4) | (4, 6) | (4, 7) | (5, 6) | (6, 7) |
| 비용 | 29 | 75 | 35 | 34 | 7 | 23 | 13 | 53 | 25 |
| 순서 | step 5 | step 1 | step 3 | step 2 | step 4 |
현재 존재하는 집합: (3, 4, 6, 7), (1, 2)
6️⃣ 2와 6을 선택합니다. 이 둘도 집합에 포함되어 있지 않으므로 서로 집합에 포함시킵니다.
| 간선 | (1, 2) | (1, 5) | (2, 3) | (2, 6) | (3, 4) | (4, 6) | (4, 7) | (5, 6) | (6, 7) |
| 비용 | 29 | 75 | 35 | 34 | 7 | 23 | 13 | 53 | 25 |
| 순서 | step 5 | step 6 | step 1 | step 3 | step 2 | step 4 |
현재 존재하는 집합: (3, 4, 6, 7, 1, 2)
7️⃣ 2와 3을 살폈을 때 이들은 이미 집합에 포함되어 있으므로 간선을 제거합니다.

| 간선 | (1, 2) | (1, 5) | (2, 3) | (2, 6) | (3, 4) | (4, 6) | (4, 7) | (5, 6) | (6, 7) |
| 비용 | 29 | 75 | 35 | 34 | 7 | 23 | 13 | 53 | 25 |
| 순서 | step 5 | step 7 | step 6 | step 1 | step 3 | step 2 | step 4 |
현재 존재하는 집합: (3, 4, 6, 7, 1, 2)
8️⃣ 5, 6의 간선을 선택합니다. 5, 6은 같은 집합에 속해 있지 않기 때문에 집합에 포함시킵니다.
| 간선 | (1, 2) | (1, 5) | (2, 3) | (2, 6) | (3, 4) | (4, 6) | (4, 7) | (5, 6) | (6, 7) |
| 비용 | 29 | 75 | 35 | 34 | 7 | 23 | 13 | 53 | 25 |
| 순서 | step 5 | step 7 | step 6 | step 1 | step 3 | step 2 | step 8 | step 4 |
현재 존재하는 집합: (1, 2, 3, 4, 5, 6, 7)
9️⃣ 마지막 간선인 (1, 5)를 선택합니다. 이들은 이미 집합에 포함되어 있기에 간선을 제거합니다.

| 간선 | (1, 2) | (1, 5) | (2, 3) | (2, 6) | (3, 4) | (4, 6) | (4, 7) | (5, 6) | (6, 7) |
| 비용 | 29 | 75 | 35 | 34 | 7 | 23 | 13 | 53 | 25 |
| 순서 | step 5 | step 9 | step 7 | step 6 | step 1 | step 3 | step 2 | step 8 | step 4 |
마지막 그래프가 크루스칼 알고리즘 과정을 거친 최종 그래프입니다.
✏️ 예제 코드
import java.util.ArrayList;
import java.util.Collections;
import java.util.Scanner;
class Edge implements Comparable<Edge> {
private final int distance;
private final int nodeA;
private final int nodeB;
public Edge(int distance, int nodeA, int nodeB) {
this.distance = distance;
this.nodeA = nodeA;
this.nodeB = nodeB;
}
public int getDistance() {
return this.distance;
}
public int getNodeA() {
return this.nodeA;
}
public int getNodeB() {
return this.nodeB;
}
// 거리(비용)가 짧은 것이 높은 우선순위를 가지도록 설정
@Override
public int compareTo(Edge other) {
if (this.distance < other.distance) {
return -1;
}
return 1;
}
}
public class Main {
// 노드의 개수(V)와 간선(Union 연산)의 개수(E)
// 노드의 개수는 최대 100,000개라고 가정
public static int v, e;
public static int[] parent = new int[100001]; // 부모 테이블 초기화하기
// 모든 간선을 담을 리스트와, 최종 비용을 담을 변수
public static ArrayList<Edge> edges = new ArrayList<>();
public static int result = 0;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
v = sc.nextInt();
e = sc.nextInt();
// 부모 테이블상에서, 부모를 자기 자신으로 초기화
for (int i = 1; i <= v; ++i) {
parent[i] = i;
}
// 모든 간선에 대한 정보를 입력 받기
for (int i = 0; i < e; ++i) {
int a = sc.nextInt();
int b = sc.nextInt();
int cost = sc.nextInt();
edges.add(new Edge(cost, a, b));
}
// 간선을 비용순으로 정렬
Collections.sort(edges);
// 간선을 하나씩 확인하며
for (Edge edge : edges) {
int cost = edge.getDistance();
int a = edge.getNodeA();
int b = edge.getNodeB();
//사이클이 발생하지 않는 경우에만 집합에 포함
if (findParent(a) != findParent(b)) {
unionParent(a, b);
result += cost;
}
}
System.out.println(result);
}
// 두 원소가 속한 집합을 합치기
private static void unionParent(int a, int b) {
a = findParent(a);
b = findParent(b);
if (a < b) {
parent[b] = a;
} else {
parent[a] = b;
}
}
// 특정 원소가 속한 집합을 찾기
private static int findParent(int x) {
// 루트 노드가 아니라면, 루트 노드를 찾을 때까지 재귀적으로 호출
if (x == parent[x]) {
return x;
}
return parent[x] = findParent(parent[x]);
}
}'알고리즘' 카테고리의 다른 글
| [프로그래머스/Java] 179963 추억 점수 (1) | 2024.10.23 |
|---|---|
| [프로그래머스/Java] 148653 마법의 엘리베이터 (0) | 2024.10.08 |
| [프로그래머스/Java] 42885 구명보트 (0) | 2024.10.02 |
| [프로그래머스/Java] 214288 상담원 인원 (0) | 2024.08.31 |
| [프로그래머스/Java] 42883 큰 수 만들기 (0) | 2024.08.30 |
