| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 |
- 등산코스 정하기
- 소프티어
- 인턴십
- 오블완
- 해결
- MySQL
- 카카오
- 설명
- softeer
- java
- 수료
- 싸피
- 퍼즐 조각 채우기
- 정기 코딩 인증평가
- 백준
- 후기
- 핵심
- 10기
- 프로그래머스
- 142085
- SQL
- 14942
- SSAFY
- 24955
- 카카오코드 본선
- 산 모양 타일링
- 티스토리챌린지
- PCCP
- 숫자 이어 붙이기
- 배열 돌리기 5
- Today
- Total
개발 쥬스
[프로그래머스/Java] 산 모양 타일링 (2024 카카오 인턴 기출 문제) 본문
🔗 문제 링크: https://school.programmers.co.kr/learn/courses/30/lessons/258705
프로그래머스
SW개발자를 위한 평가, 교육, 채용까지 Total Solution을 제공하는 개발자 성장을 위한 베이스캠프
programmers.co.kr
🔍 해결 과정
문제를 보았을 때 dp를 활용하여 문제를 해결해야겠다는 생각을 가지긴 했지만, 어떤 것을 기준으로 잡아서 점화식을 세우는 것이 적절한지 고민이 많았던 문제였습니다.
그렇게 몇 시간 동안 고민한 끝에 타일의 오른쪽 맨 끝 삼각형을 기준으로 잡고 이 삼각형이 마름모로 묶여 있는 경우와 묶여 있지 않는 경우 두 가지 경우를 생각해서 점화식을 세웠습니다. 즉 2차원 배열의 dp를 활용하여 마름모 또는 정삼각형으로 타일에서 채울 수 있는 경우의 수를 계산하였습니다. 정의를 하자면 다음과 같습니다.
1️⃣ dp[i][0]: 아랫쪽 맨 오른쪽 삼각형의(i번째 삼각형, 0번부터 시작)에서 마름모로 묶여 있지 않았을 때의 적용할 수 있는 경우의 수
2️⃣ dp[i][1]: 아랫쪽 맨 오른쪽 삼각형의(i번째 삼각형, 0번부터 시작)에서 마름모로 묶였을 때의 적용할 수 있는 경우의 수
3️⃣ dp[i][0] + dp[i][1] = 타일 맨 오른쪽 삼각형(i 번째 인덱스)에서 타일에 적용할 수 있는 경우의 수
하지만 사다리꼴 특정 위치에 정삼각형이 존재하는 경우와 존재하지 않는 경우가 제각각이므로 이들에 대한 점화식을 각각 따로 적용해야합니다.
💡 마지막 타일에서 맨 오른쪽 정삼각형이 마름모로 묶여 있지 않고, 위에 정삼각형이 없는 경우
먼저 아래 그림과 같이 사다리꼴에서 맨 오른쪽 위에 삼각형이 존재하지 않는 타일의 경우를 생각해봅시다.

이 경우에서 먼저 마름모로 묶여 있지 않는 경우를 생각해봅시다. 그림 1에서 맨 오른쪽에 있는 정삼각형의 위치는 i번 인덱스가 됩니다.
점화식을 위해 다음과 같이 두 가지 상황을 고려해야합니다.
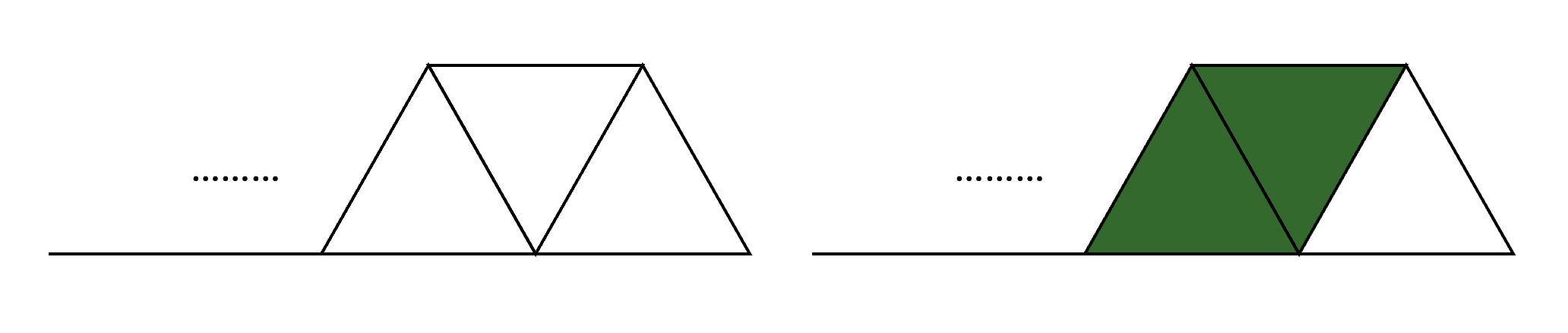
그림 2의 왼쪽 그림에서 점화식을 생각한다면 마름모로 묶여 있지 않고 단순히 오른쪽으로 타일이 두 개가 생긴 것 뿐이므로 이전 점화식의 경우가 한 번 더 생긴 경우와 같습니다. 그래서 왼쪽 그림에 대한 점화식을 표현하자면 다음과 같습니다.
dp[i - 1][0] + dp[i - 1][1] (이전의 경우가 추가)
그림 2의 오른쪽 그림의 경우는 앞의 두 정삼각형이 마름모로 묶여 있는 경우입니다. 이 경우에서 점화식을 세울 때 헷갈릴 수도 있겠지만 자세히 생각하면 이 경우의 수는 그 이전 인덱스의 맨 오른쪽 정삼각형(즉 오른쪽 그림에서 맨 왼쪽 삼각형)이 마름모로 묶여 있지 않는 경우의 수와 같습니다.
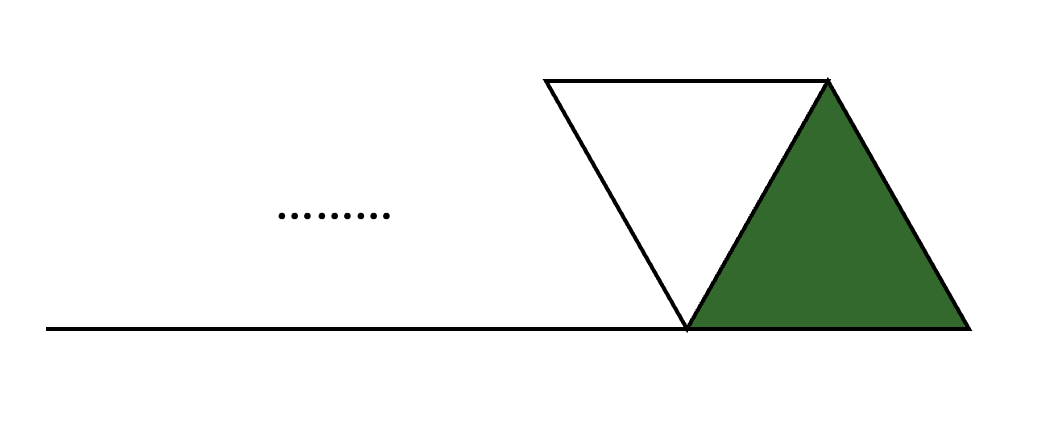
오른쪽 그림에서 그 이전 인덱스의 정삼각형만을 기준으로 그림을 다시 가져왔을 때의 상황입니다. 여기서 맨 오른쪽 정삼각형 하나만 단순히 칠해진 상황이고, 그 앞의 정삼각형과 마름모로 이어질 일이 없기에 이는 마름모로 묶여 있지 않았을 때의 타일의 경우와 같음을 알 수가 있습니다.
따라서 그림 2에서 오른쪽 그림에 대한 점화식을 표현하자면 다음과 같습니다.
dp[i - 1][0]
결국 마름모로 묶여 있지 않고, 현재 위치에서 위쪽에 정삼각형이 존재하지 않을 때의 점화식은 다음과 같습니다.
dp[i][0] (위쪽에 정삼각형이 존재하지 않고, 마름모로 묶여 있지 않는 경우) = dp[i - 1][0] + dp[i - 1][1] + dp[i - 1][0]
💡 마지막 타일에서 맨 오른쪽 정삼각형이 마름모로 묶여 있고, 위에 정삼각형이 없는 경우
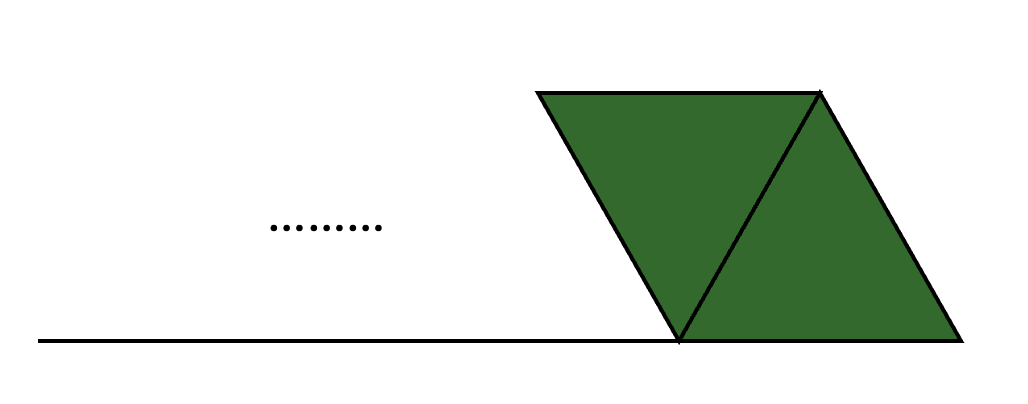
이 경우에는 이전 인덱스의 정삼각형 타일에서의 경우의 수가 추가된 것과 같으므로 점화식을 표현하면 다음과 같습니다.
dp[i][0] = dp[i - 1][0] + dp[i - 1][1] (이전의 경우의 수가 한 번 추가된 것.)
💡 마지막 타일에서 맨 오른쪽 정삼각형이 마름모로 묶여 있지 않고, 위에 정삼각형이 있는 경우
아래 그림과 같이 다음 세 가지 상황을 고려해야 합니다.
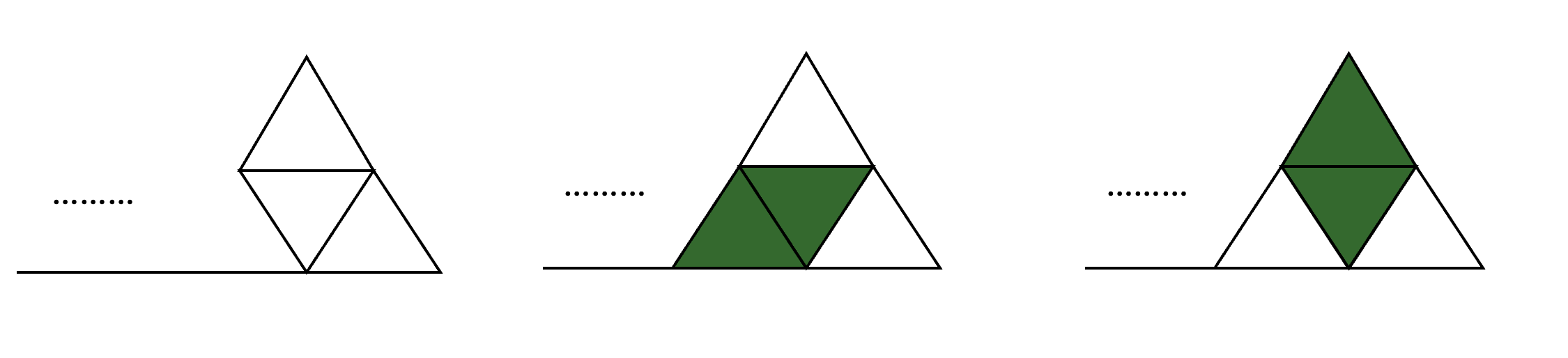
그림 5의 왼쪽 경우에서는 다음과 같은 상황으로 계산할 수 있습니다.
그림 5의 왼쪽 그림에서 나올 수 있는 경우: dp[i - 1][0] + dp[i - 1][1] (이전 인덱스에서의 경우와 같다.)
그림 5의 중간 경우에서는 그 이전 상황에서의 맨 오른쪽 정삼각형이 마름모로 묶여 있지 않는 상황과 같습니다.
그림 5의 중간 그림에서 나올 수 있는 경우: dp[i - 1][0]
그림 5의 오른쪽 그림은 그 이전의 인덱스의 정삼각형에서의 상황이 한 번 더 추가된 것과 같습니다.
그림 5의 오른쪽 그림에서 나올 수 있는 경우: dp[i - 1][0] + dp[i - 1][1]
따라서 최종 경우를 점화식으로 표현하자면 다음과 같습니다.
dp[i][0] (위에 정삼각형이 있고, 마름모로 묶여 있지 않는 경우) = dp[i - 1][0] * 3 + dp[i - 1][1] * 2
💡 마지막 타일에서 맨 오른쪽 정삼각형이 마름모로 묶여 있는 경우 (위에 정삼각형 유무 상관 없음)
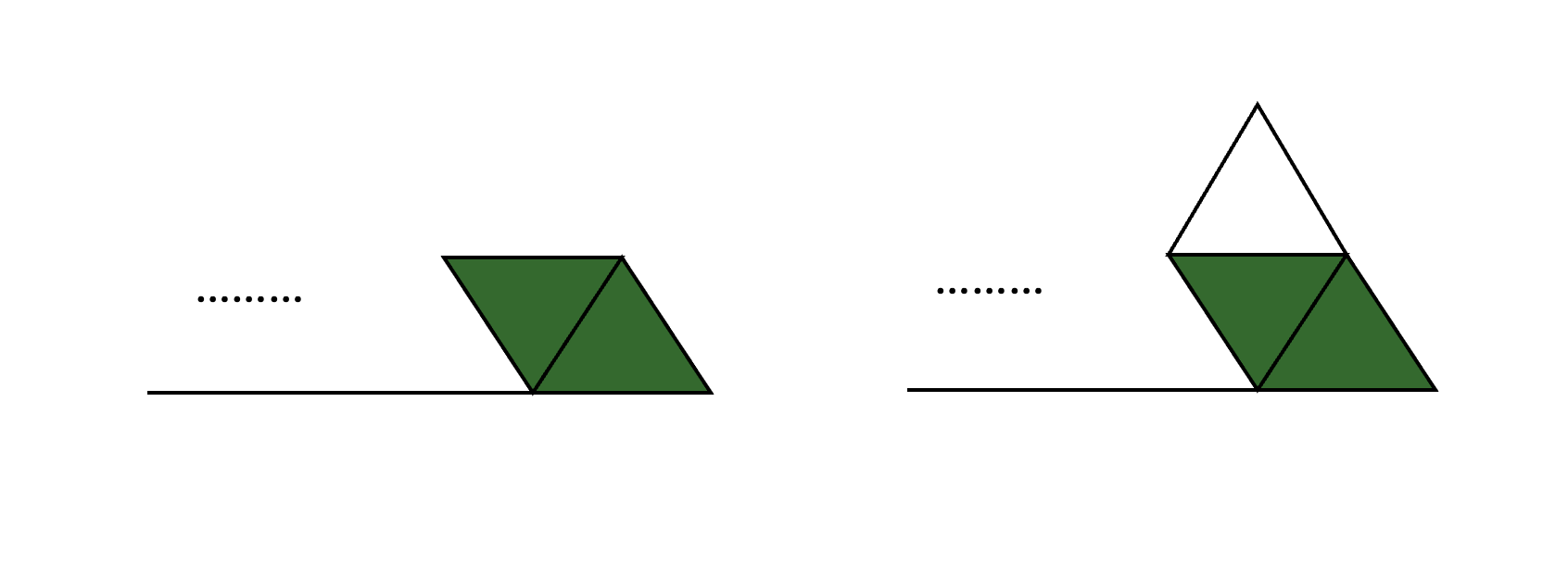
그림 6의 상황은 그 이전의 상황의 경우가 한번 더 생긴 것과 같으므로 다음과 같이 점화식을 세울 수가 있습니다.
dp[i][1] = dp[i - 1][0] + dp[i - 1][1] (맨 오른쪽 정삼각형이 마름모로 묶여 있는 경우 위의 정삼각형 유무와 상관 없이 이전의 경우의 수가 한 번 더 생긴 것과 같다.)
bottom-up 방식을 통해서 각 경우에 따라서 적절한 점화식을 통해서 경우를 계산해 준 다음, 최종 타일에서의 경우를 반환해주면 됩니다.
✏️ 코드
import java.util.*;
class Solution {
private static final int MOD = 10007;
private static final int NOTHING = 0;
public int solution(int n, int[] tops) {
int[][] dp = new int[n + 1][2];
dp[0][0] = 1;
for (int i = 0; i < n; ++i) {
int top = tops[i];
dp[i + 1][1] = (dp[i][0] + dp[i][1]) % MOD;
if (top == NOTHING) {
dp[i + 1][0] = (dp[i][0] * 2 + dp[i][1]) % MOD;
} else {
dp[i + 1][0] = (dp[i][0] * 3 + dp[i][1] * 2) % MOD;
}
}
return (dp[n][0] + dp[n][1]) % MOD;
}
}'알고리즘' 카테고리의 다른 글
| [프로그래머스/MySQL] 상품 별 오프라인 매출 구하기 (1) | 2025.01.15 |
|---|---|
| [SWEA/Java] (SW Expert Academy) 1249 보급로 (0) | 2025.01.10 |
| [백준/Java] 17470 배열 돌리기 5 (0) | 2025.01.05 |
| [백준/Java] 13460 구슬 탈출 2 (0) | 2024.12.11 |
| [백준/Java] 9202 Boggle (1) | 2024.12.11 |

